RelaçõEs MéTricas No TriâNgulo RetâNgulo Formulas E Exemplos

Relações Métricas No Triângulo Retângulo Formulas E Exemplos – Relações Métricas No Triângulo Retângulo: Fórmulas e Exemplos, este estudo aprofunda a compreensão das relações geométricas que regem os triângulos retângulos, explorando as fórmulas que permitem calcular lados, alturas e áreas, e ilustrando sua aplicação em diversos exemplos práticos.

O estudo das relações métricas no triângulo retângulo tem raízes profundas na história da matemática, remontando à civilização babilônica e egípcia. A aplicação dessas relações é fundamental em diversas áreas do conhecimento, como engenharia, arquitetura, física e astronomia, sendo crucial para o cálculo de distâncias, alturas e ângulos em situações reais.

Introdução às Relações Métricas no Triângulo Retângulo

As relações métricas no triângulo retângulo são ferramentas essenciais para a resolução de problemas que envolvem triângulos retângulos, com aplicações em diversas áreas como engenharia, arquitetura, física e matemática. Essas relações estabelecem conexões entre os lados e as alturas do triângulo, permitindo calcular medidas desconhecidas e analisar propriedades geométricas.

A história do estudo das relações métricas no triângulo retângulo remonta à Grécia Antiga, com os trabalhos de Pitágoras e Euclides. Pitágoras, conhecido pelo famoso teorema que leva seu nome, desenvolveu a relação fundamental entre os lados do triângulo retângulo, estabelecendo que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos.

Euclides, em seus “Elementos”, aprofundou o estudo das relações métricas, incluindo teoremas e proposições que descrevem as relações entre os segmentos formados pela altura relativa à hipotenusa e as projeções dos catetos sobre a hipotenusa.

Conceitos Fundamentais, Relações Métricas No Triângulo Retângulo Formulas E Exemplos

As relações métricas no triângulo retângulo se baseiam em conceitos fundamentais relacionados aos elementos do triângulo:

• Catetos:Os lados que formam o ângulo reto do triângulo retângulo.
• Hipotenusa:O lado oposto ao ângulo reto, sendo o maior lado do triângulo retângulo.
• Altura:O segmento de reta perpendicular à hipotenusa, traçado do vértice do ângulo reto.
• Projeções:Os segmentos de reta formados pela altura sobre a hipotenusa, que representam as projeções dos catetos sobre a hipotenusa.
• Área:A medida da superfície do triângulo retângulo, calculada pela metade do produto da base pela altura.

Teorema de Pitágoras

O Teorema de Pitágoras é uma das relações métricas mais importantes no estudo dos triângulos retângulos. Ele estabelece uma relação fundamental entre os lados de um triângulo retângulo, definindo que a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.

Demonstração do Teorema de Pitágoras

A demonstração do Teorema de Pitágoras pode ser feita de diversas maneiras, mas uma das mais simples e intuitivas é a seguinte:

Construção

Considere um triângulo retângulo ABC, onde AB e AC são os catetos e BC é a hipotenusa. Construa quadrados sobre cada lado do triângulo, como mostra a figura abaixo.

Relação de áreas

Observe que a área do quadrado construído sobre a hipotenusa (BC) é igual à soma das áreas dos quadrados construídos sobre os catetos (AB e AC). Isso ocorre porque podemos dividir o quadrado sobre a hipotenusa em quatro triângulos retângulos congruentes ao triângulo original, e um quadrado menor no centro, cuja área é igual à área do quadrado construído sobre o cateto menor.

Fórmula

A área de um quadrado é calculada multiplicando o lado por ele mesmo. Portanto, podemos escrever a relação de áreas da seguinte forma:

BC² = AB² + AC²

Essa fórmula representa o Teorema de Pitágoras: o quadrado da hipotenusa é igual à soma dos quadrados dos catetos.

Aplicações do Teorema de Pitágoras

O Teorema de Pitágoras tem diversas aplicações práticas em áreas como:

Engenharia

Na construção de pontes, edifícios e outras estruturas, o Teorema de Pitágoras é usado para calcular o comprimento de vigas, pilares e outros elementos estruturais.

Navegação

Na navegação marítima e aérea, o Teorema de Pitágoras é usado para calcular distâncias e direções.

Geometria Analítica

Em geometria analítica, o Teorema de Pitágoras é usado para calcular a distância entre dois pontos no plano cartesiano.

Física

O Teorema de Pitágoras é usado em física para calcular a magnitude de vetores, como velocidade e força.

Exemplos Práticos do Teorema de Pitágoras

Calcular a distância entre dois pontos

Imagine que você precisa calcular a distância entre dois pontos A e B em um mapa. Você pode usar o Teorema de Pitágoras para calcular a distância em linha reta entre os dois pontos, considerando a distância horizontal como um cateto e a distância vertical como outro cateto.

Calcular a altura de um edifício

Imagine que você precisa calcular a altura de um edifício. Você pode usar o Teorema de Pitágoras para calcular a altura, considerando a distância do edifício até um ponto de referência no chão como um cateto e a distância do ponto de referência até o topo do edifício como a hipotenusa.

Calcular o comprimento de uma escada

Imagine que você precisa calcular o comprimento de uma escada para alcançar o telhado de uma casa. Você pode usar o Teorema de Pitágoras para calcular o comprimento da escada, considerando a altura da casa como um cateto e a distância da base da casa até a parede como outro cateto.

Relações Métricas Básicas

As relações métricas no triângulo retângulo são fórmulas que relacionam os lados e a altura do triângulo, permitindo calcular medidas desconhecidas. Essas relações são fundamentadas na semelhança de triângulos e no Teorema de Pitágoras.

Altura, Catetos e Hipotenusa

A altura de um triângulo retângulo é o segmento de reta perpendicular à hipotenusa, traçado a partir do vértice do ângulo reto. A altura divide o triângulo retângulo em dois triângulos menores, também retângulos, semelhantes ao triângulo original.

• A altura é a média geométrica dos segmentos que ela determina sobre a hipotenusa. Isso significa que o quadrado da altura é igual ao produto dos segmentos da hipotenusa.
• A altura também é a média geométrica dos catetos. Ou seja, o quadrado da altura é igual ao produto dos catetos.

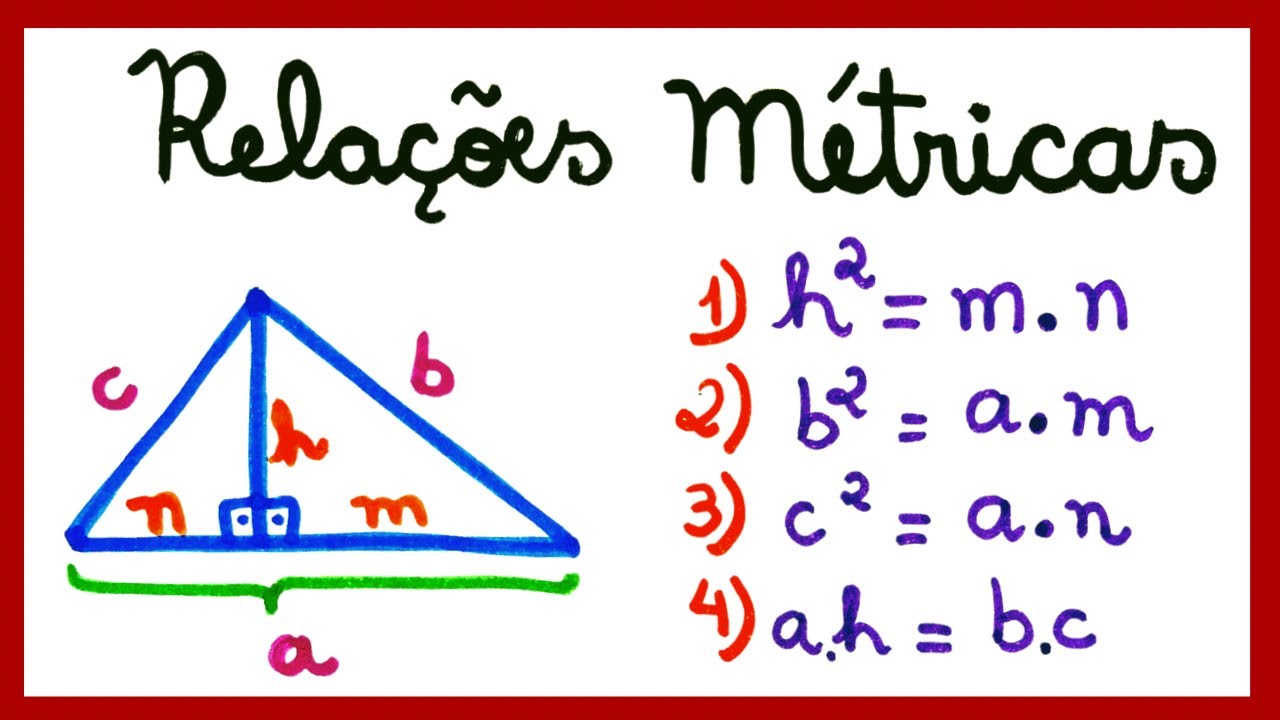
h² = m.nh² = b.c

Onde:

• h é a altura
• m e n são os segmentos da hipotenusa
• b e c são os catetos

Projeções dos Catetos sobre a Hipotenusa

As projeções dos catetos sobre a hipotenusa são os segmentos da hipotenusa determinados pela altura.

• O quadrado de um cateto é igual ao produto da hipotenusa pela sua projeção sobre a hipotenusa.
• A razão entre as projeções dos catetos sobre a hipotenusa é igual ao quadrado da razão entre os catetos.

b² = a.mc² = a.nm/n = b²/c²

Onde:

• a é a hipotenusa
• m e n são as projeções dos catetos b e c sobre a hipotenusa, respectivamente.

Semelhança de Triângulos

A semelhança de triângulos é fundamental para derivar as relações métricas.

• O triângulo retângulo original e os dois triângulos menores formados pela altura são semelhantes.
• A semelhança entre os triângulos permite estabelecer proporções entre os lados correspondentes.
• Essas proporções levam às relações métricas descritas anteriormente.

ΔABC ~ ΔAHB ~ ΔACH

Onde:

• ΔABC é o triângulo retângulo original
• ΔAHB e ΔACH são os triângulos menores formados pela altura

Aplicações das Relações Métricas: Relações Métricas No Triângulo Retângulo Formulas E Exemplos

As relações métricas no triângulo retângulo são ferramentas poderosas para resolver problemas que envolvem medidas de lados, alturas e projeções em triângulos retângulos. Essas relações permitem calcular comprimentos desconhecidos, áreas e outras grandezas geométricas, tornando-se essenciais em diversas áreas da matemática, engenharia e física.

Relações Métricas no Triângulo Retângulo: Tabela de Fórmulas

Para facilitar a aplicação das relações métricas, a tabela a seguir resume as principais fórmulas, incluindo a altura, as projeções e as áreas:

Fórmula	Descrição
h² = m.n	O quadrado da altura relativa à hipotenusa é igual ao produto das projeções dos catetos sobre a hipotenusa.
a² = c.m	O quadrado de um cateto é igual ao produto da hipotenusa pela projeção desse cateto sobre a hipotenusa.
b² = c.n	O quadrado do outro cateto é igual ao produto da hipotenusa pela projeção desse cateto sobre a hipotenusa.
a² + b² = c²	Teorema de Pitágoras: O quadrado da hipotenusa é igual à soma dos quadrados dos catetos.
Área do Triângulo = (b.h)/2	A área de um triângulo é igual à metade do produto da base pela altura.

Resolvendo Problemas com Relações Métricas

As relações métricas podem ser usadas para resolver uma variedade de problemas, como:

• Determinar o comprimento de um lado desconhecido em um triângulo retângulo.
• Calcular a altura de um triângulo retângulo.
• Encontrar as projeções dos catetos sobre a hipotenusa.
• Calcular a área de um triângulo retângulo.

Exemplo 1: Encontrando o Comprimento de um Lado Desconhecido

Considere um triângulo retângulo ABC, onde AB é a hipotenusa, AC é um cateto e BC é o outro cateto. Se AB = 10 cm e AC = 6 cm, encontre o comprimento de BC.

Aplicando o Teorema de Pitágoras, temos:

AB² = AC² + BC²

Substituindo os valores conhecidos:

² = 6² + BC²

Resolvendo para BC:

BC² = 10²

6² = 64

Portanto, BC = √64 = 8 cm.

Exemplo 2: Encontrando a Altura de um Triângulo Retângulo

Considere um triângulo retângulo ABC, onde AB é a hipotenusa, AC é um cateto e BC é o outro cateto. Se AB = 12 cm e AC = 9 cm, encontre a altura relativa à hipotenusa (h).

Aplicando a relação h² = m.n, onde m e n são as projeções dos catetos sobre a hipotenusa, temos:

h² = m.n

Para encontrar m e n, podemos usar as relações a² = c.m e b² = c.n. Substituindo os valores conhecidos:

² = 12.m

m = 9²/12 = 6,75 cm

b² = 12.n

n = b²/12 = 12²

9² / 12 = 5,25 cm

Agora, podemos calcular a altura:

h² = 6,75.5,25

h = √(6,75.5,25) = 5,9 cm

Exemplo 3: Encontrando as Projeções dos Catetos sobre a Hipotenusa

Considere um triângulo retângulo ABC, onde AB é a hipotenusa, AC é um cateto e BC é o outro cateto. Se AB = 15 cm e h = 6 cm, encontre as projeções dos catetos sobre a hipotenusa (m e n).

Aplicando a relação h² = m.n, temos:

² = m.n

Para encontrar m e n, podemos usar as relações a² = c.m e b² = c.n. Substituindo os valores conhecidos:

a² = 15.m

b² = 15.n

Somando as duas equações:

a² + b² = 15.m + 15.n

Pelo Teorema de Pitágoras, a² + b² = c² = 15², então:

² = 15.m + 15.n

Simplificando:

= m + n

Agora, temos duas equações:

² = m.n

= m + n

Resolvendo esse sistema de equações, encontramos m = 9 cm e n = 6 cm.

Relações Métricas e Trigonometria

As relações métricas no triângulo retângulo e as funções trigonométricas, embora pareçam distintas, estão profundamente interligadas. Essa conexão permite que os conceitos de uma área sejam aplicados à outra, expandindo as ferramentas disponíveis para resolver problemas geométricos.

Relações entre Relações Métricas e Funções Trigonométricas

As relações métricas no triângulo retângulo fornecem fórmulas que relacionam os lados e as alturas do triângulo. As funções trigonométricas, por outro lado, relacionam os ângulos e os lados de um triângulo retângulo. A conexão entre as duas reside no fato de que as relações métricas podem ser usadas para expressar as funções trigonométricas em termos dos lados do triângulo.

Calculando Seno, Cosseno e Tangente Usando Relações Métricas

Considere um triângulo retângulo ABC, com ângulo reto em C. Sejam a, b e c os comprimentos dos lados opostos aos ângulos A, B e C, respectivamente. Sejam h a altura relativa à hipotenusa c e m e n as projeções dos catetos a e b sobre a hipotenusa, respectivamente.

As relações métricas fornecem as seguintes fórmulas:

• a² = c- m
• b² = c – n
• h² = m – n

As funções trigonométricas seno, cosseno e tangente são definidas como:

• sen A = a/c
• cos A = b/c
• tg A = a/b

Usando as relações métricas, podemos expressar essas funções em termos de m e n:

• sen A = √(m/c)
• cos A = √(n/c)
• tg A = √(m/n)

Portanto, as relações métricas podem ser usadas para calcular os valores de seno, cosseno e tangente de um ângulo em um triângulo retângulo, conhecendo os comprimentos dos seus lados.

Diagrama Ilustrativo

[Diagrama que ilustra um triângulo retângulo ABC, com a hipotenusa c, os catetos a e b, a altura h, e as projeções m e n. As fórmulas das relações métricas e as funções trigonométricas são indicadas no diagrama, mostrando a relação entre elas.]

Exemplos e Aplicações Práticas

As relações métricas no triângulo retângulo têm aplicações práticas em diversas áreas, como engenharia, arquitetura e navegação. Essas relações permitem calcular distâncias, alturas e ângulos em situações reais, tornando-se ferramentas essenciais para solucionar problemas práticos.

Engenharia Civil

As relações métricas são amplamente utilizadas em projetos de engenharia civil, como na construção de pontes, edifícios e estradas. Por exemplo, para calcular a altura de um edifício, um engenheiro pode utilizar o teorema de Pitágoras, relacionando a altura do edifício com a distância horizontal até o edifício e a distância da base do edifício até o ponto de observação.

O teorema de Pitágoras afirma que em um triângulo retângulo, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos.

Arquitetura

Na arquitetura, as relações métricas são usadas para projetar estruturas e calcular as dimensões de diferentes elementos, como telhados, escadas e janelas. Por exemplo, para calcular o comprimento de uma escada, um arquiteto pode utilizar as relações métricas para determinar o comprimento da escada em função da altura do degrau e do ângulo da escada.

Navegação

Na navegação, as relações métricas são usadas para determinar a distância entre dois pontos, a direção de um destino e a velocidade de um navio ou avião. Por exemplo, um navegador pode utilizar as relações métricas para calcular a distância entre dois pontos no mar, usando a latitude e a longitude dos dois pontos.

Exemplo Prático

Imagine que você precisa calcular a altura de uma árvore. Você sabe que a distância da base da árvore até o ponto onde você está é de 10 metros e o ângulo de elevação da árvore é de 30 graus.

Utilizando as relações métricas, você pode calcular a altura da árvore da seguinte forma:* Desenhe um diagrama:Desenhe um triângulo retângulo com a árvore como a altura, a distância da base da árvore até você como a base e a linha de visão como a hipotenusa.

Identifique os lados e ângulos

A altura da árvore é o cateto oposto ao ângulo de 30 graus, a distância da base da árvore até você é o cateto adjacente ao ângulo de 30 graus e a linha de visão é a hipotenusa.

Utilize a tangente

A tangente de um ângulo é igual ao cateto oposto dividido pelo cateto adjacente. Neste caso, a tangente de 30 graus é igual à altura da árvore dividida pela distância da base da árvore até você.

Calcule a altura

Substituindo os valores conhecidos, temos: tan(30°) = altura / 10 metros. Resolvendo para a altura, obtemos: altura = 10 metros

tan(30°) = 5,77 metros.

Portanto, a altura da árvore é de aproximadamente 5,77 metros.

Expert Answers

Quais são as principais relações métricas no triângulo retângulo?

As principais relações métricas no triângulo retângulo incluem o Teorema de Pitágoras, que relaciona os quadrados dos catetos com o quadrado da hipotenusa, e as relações entre a altura, os catetos, as projeções dos catetos sobre a hipotenusa e a hipotenusa.

Como as relações métricas são aplicadas na resolução de problemas práticos?

As relações métricas são aplicadas na resolução de problemas práticos em diversas áreas, como a engenharia, a arquitetura e a navegação. Por exemplo, podem ser utilizadas para calcular a altura de um edifício, a distância entre dois pontos ou o ângulo de inclinação de uma rampa.